pathDeformation.py

A module for finding instantons between vacua in multiple field dimensions.

The basic strategy is an iterative process:

1. Make an ansatz for the path along which the field will travel.
2. Split up the equations of motion into components that are parallel and perpendicular to the direction of travel along the path.
3. The direction of motion parallel to the path reduces to a one-dimensional equation of motion, which can be solved using the overshoot / undershoot techniques in tunneling1D. Solve it.
4. Treating the motion of the field as a classical particle moving in an inverted potential, calculate the normal forces that would need to act on the particle to keep it on the path. If this forces are (close enough to) zero, the ansatz was correctly. Otherwise iteratively deform the path in the direction of the normal forces, stopping when the forces go to zero.
5. Loop back to step 3 until no further deformation is necessary.

The classes Deformation_Spline and Deformation_Points will perform step 3, while fullTunneling() will run the entire loop.

For more explicit details, see the original paper Comput. Phys. Commun. 183 (2012) [arXiv:1109.4189].

Deformation classes

exception DeformationError

Raised when path deformation fails.

class Deformation_Spline(phi, dphidr, dV, nb=10, kb=3, v2min=0.0, fix_start=False, fix_end=False, save_all_steps=False)

Bases: object

Deform a path in the presence of a potential such that the normal forces along the path are zero.

This class fits a spline to the points, and does the actual deformation on the spline rather than on the points themselves. This make the path somewhat smoother than it would otherwise be (which is generally desirable), but it does make it difficult to resolve sharp turns in the path.

Parameters:

• phi (array_like) – The list of points that constitutes the original path. Should have shape (n_points, n_dimensions).
• dphidr (array_like) – The ‘speed’ along the path at the initial points. This does not change as the path deforms. Should have shape (n_points,). Gets saved into the attribute v2 as v2 = dphidr[:,np.newaxis]**2.
• dV (callable) – The potential gradient as a function of phi. The output shape should be the same as the input shape, which will be (..., n_dimensions).
• nb (int, optional) – Number of basis splines to use.
• kb (int, optional) – Order of basis splines.
• v2min (float, optional) – The smallest the square of dphidr is allowed to be, relative to the characteristic force exterted by F_ext. Note that the self-correcting nature of the deformation goes away when dphidr=0.
• fix_end (fix_start,) – If True, the force on the first/last point along the path is set to zero, so the point will not change in the deformation step.
• save_all_steps (bool, optional) – If True, each step gets saved into self.phi_list and self.F_list.

Variables:

• phi (array_like) – Set during initialization, and then rewritten at each step.
• num_steps (int) – Total number of steps taken.

forces()

Calculate the normal force and potential gradient on the path.

Returns:F_norm, dV (array_like)

step(lastStep, maxstep=0.1, minstep=0.0001, reverseCheck=0.15, stepIncrease=1.5, stepDecrease=5.0, checkAfterFit=True, verbose=False)

Deform the path one step.

Each point is pushed in the direction of the normal force - the force that the path exerts on a classical particle moving with speed dphidr in a potential with gradient dV such that the particle stays on the path. A stepsize of 1 corresponds to moving the path an amount L*N/(dV_max), where L is the length of the (original) path, N is the normal force, and dV_max is the maximum force exerted by the potential along the path.

Parameters:

• lastStep (float) – Size of the last step.
• minstep (maxstep,) –
• reverseCheck (float, optional) – Percentage of points for which the force can reverse direcitons (relative to the last step) before the stepsize is decreased. If reverseCheck >= 1, the stepsize is kept at lastStep.
• stepDecrease (stepIncrease,) – The amount to increase or decrease stepsize over the last step. Both should be bigger than 1.
• checkAfterFit (bool, optional) – If True, the convergence test is performed after the points are fit to a spline. If False, it’s done beforehand.
• verbose (bool, optional) – If True, output is printed at each step.

Returns:

• stepsize (float) – The stepsize used for this step.
• step_reversed (bool) – True if this step was reversed, otherwise False
• fRatio (float) – The ratio of the maximum normal force to the maximum potential gradient. When the path is a perfect fit, this should go to zero. If checkAfterFit == True, the normal force in this ratio is defined by the change in phi this step after being fit to a spline. Note that if the spline does a poor job of fitting the points after the deformation in this step (which might be the case if there are not enough basis functions), and if checkAfterFit == False, this ratio can be non-zero or large even if there is no change in phi.

Notes

In prior versions of this function (CosmoTransitions v1.0.2 and earlier), the start and end points of the path were effectively held fixed during the main deformation. This was because the line phi_lin = phi[:1] + ... was calculated before the line phi = phi+F*stepsize. Since the spline basis functions are zero at the start and end points (the spline is added on top of the straight line between the end points), when the points were later taken from the spline the end points wouldn’t move. This was by design, since for thin-walled bubbles the endpoints should stay fixed at the two vacua. However, this caused problems for thick-walled bubbles where the end points should move.

To get around this, prior versions added an extra block of code to move the end points before the main deformation. However, this was unnecessarily complicated and led to error-prone code. In this version, the end points are always allowed to move if the force F is non-zero. In the thin-walled case, the force should be almost exactly zero at the end points anyways (there is zero potential gradient and dphidr is zero), so they should stay fixed on their own.

deformPath(startstep=0.002, fRatioConv=0.02, converge_0=5.0, fRatioIncrease=5.0, maxiter=500, verbose=True, callback=None, step_params={})

Deform the path many individual steps, stopping either when the convergence criterium is reached, when the maximum number of iterations is reached, or when the path appears to be running away from convergence.

Parameters:

• startstep (float, optional) – Starting stepsize used in step().
• fRatioConv (float, optional) – The routine will stop when the maximum normal force on the path divided by the maximum potential gradient is less than this.
• converge_0 (float, optional) – On the first step, use a different convergence criterion. Check if fRatio < convergence_0 * fRatioConv.
• fRatioIncrease (float, optional) – The maximum fractional amount that fRatio can increase before raising an error.
• maxiter (int, optional) – Maximum number of steps to take (ignoring reversed steps).
• verbose (bool, optional) – If True, print the ending condition.
• callback (callable, optional) – Called after each step. Should accept an instance of this class as a parameter, and return False if deformation should stop.
• step_params (dict, optional) – Parameters to pass to step().

Returns:

deformation_converged (bool) – True if the routine stopped because it converged (as determined by fRatioConv), False otherwise.

class Deformation_Points(phi, dphidr, dV, fix_start=False, fix_end=False, save_all_steps=False)

Bases: object

Deform a path in the presence of a potential such that the normal forces along the path are zero.

Unlike Deformation_Spline, this class changes the points themselves rather than fitting a spline to the points. It is a more straightforward implementation, and when run with comparable inputs (i.e., the number of basis splines is about the same as the number of points), this method tends to be somewhat faster. The individual stepsizes here change with the total number of points, whereas in the spline implementation they mostly depend on the number of basis functions. However, as long as the path is fairly smooth, the total number of splines in that class can probably be smaller than the total number of points in this class, so this class will tend to be somewhat slower.

The two implementations should converge upon the same answer when the number of points and basis functions get large.

Parameters:

• phi (array_like) – The list of points that constitutes the original path. Should have shape (n_points, n_dimensions).
• dphidr (array_like) – The ‘speed’ along the path at the initial points. This does not change as the path deforms. Should have shape (n_points,). Gets saved into the attribute self.v2 as v2 = dphidr[:,np.newaxis]**2.
• dV (callable) – The potential gradient as a function of phi. The output shape should be the same as the input shape, which will be (..., n_dimensions).
• fix_end (fix_start,) – If True, the force on the first/last point along the path is set to zero, so the point will not change in the deformation step.
• save_all_steps (bool, optional) – If True, each step gets saved into self.phi_list and self.F_list.

Variables:

• phi (array_like) – Set during initialization, and then rewritten at each step.
• num_steps (int) – Total number of steps taken.

forces(phi=None)

Calculate the normal force and potential gradient on the path.

Returns:F_norm, dV (array_like)

step(stepsize, minstep, diff_check=0.1, step_decrease=2.0)

Take two half-steps in the direction of the normal force.

Parameters:

• stepsize (float) – Determines change in phi: phi += F_norm*stepsize.
• minstep (float) – The smallest the stepsize is allowed to be.
• diff_check (float, optional) – The stepsize is chosen such that difference between the forces at beginning of the step and halfway through the step is small compared to the force itself: max(F2-F1) < diff_check * max(F1), where max here really means the maximum absolute value of the force in each direction.
• step_decrease (float, optional) – Amount by which to decrease the stepsize if the step is too big.

Returns:

• stepsize (float) – The stepsize used for this step.
• fRatio (float) – The ratio of the maximum normal force to the maximum potential gradient. When the path is a perfect fit, this should go to zero.

deformPath(startstep=0.1, minstep=1e-06, step_increase=1.5, fRatioConv=0.02, converge_0=5.0, fRatioIncrease=20.0, maxiter=500, verbose=1, callback=None, step_params={})

Deform the path many individual steps, stopping either when the convergence criterium is reached, when the maximum number of iterations is reached, or when the path appears to be running away from convergence.

Parameters:

• maxstep (startstep,) – Starting and maximum stepsizes used in step(), rescaled by |phi[0]-phi[1]| / (max(dV)*num_points).
• fRatioConv (float, optional) – The routine will stop when the maximum normal force on the path divided by the maximum potential gradient is less than this.
• converge_0 (float, optional) – On the first step, use a different convergence criterion. Check if fRatio < convergence_0 * fRatioConv.
• fRatioIncrease (float, optional) – The maximum fractional amount that fRatio can increase before raising an error.
• maxiter (int, optional) – Maximum number of steps to take (ignoring reversed steps).
• verbose (int, optional) – If verbose >= 1, print the ending condition. If verbose >= 2, print fRatio and stepsize at each step.
• callback (callable, optional) – Called after each step. Should accept an instance of this class as a parameter, and return False if deformation should stop.
• step_params (dict, optional) – Parameters to pass to step().

Returns:

deformation_converged (bool) – True if the routine stopped because it converged (as determined by fRatioConv), False otherwise.

SplinePath

class SplinePath(pts, V, dV=None, V_spline_samples=100, extend_to_minima=False, reeval_distances=True)

Bases: object

Fit a spline to a path in field space, and find the potential on that path.

The spline-fitting happens in several steps:

1. The derivatives of the input points are found, and used to determine the path length and direction at each point.
2. If extend_to_minima is True, additional points are added at each end of the path such that ends lie on local minima.
3. The points are fit to a spline, with the knots given by the path distances from the first point.
4. If reeval_distances is True, the distances to each point are re-evaluated using the spline. A new spline is fit with more accurate knots.

The potential as a function of distance can be defined in one of two ways. If V_spline_samples is None, the potential as a function of distance x along the path is given by V[pts(x)], where pts(x) is the spline function that defines the path. If V_spline_samples is not None, the potential is first evaluated V_spline_samples times along the path, and another spline is fit to the output. In other words, when V_spline_samples is None, the input potential V is evaluated for every value x passed to to the class method V(), whereas if V_spline_samples is not None, the input potential is only evaluated during initialization.

Parameters:

• pts (array_like) – The points that describe the path, with shape (num_points, N_dim).
• V (callable) – The potential function. Input arrays will be shape (npts, N_dim) and output should have shape (npts,). Can be None.
• dV (callable, optional.) – The gradient of the potential. Input arrays will be shape (npts, N_dim) and output should have shape (npts, N_dim). Only used if V_spline_samples=None.
• V_spline_samples (int or None, optional) – Number of samples to take along the path to create the spline interpolation functions. If None, the potential is evaluated directly from V given in the input. If not None, V_spline_samples should be large enough to resolve the smallest features in the potential. For example, the potential may have a very narrow potential barrier over which multiple samples should be taken.
• extend_to_minima (bool, optional) – If True, the input path is extended at each end until it hits local minima.
• reeval_distances (bool, optional) – If True, get more accurate distances to each knot by integrating along the spline.

Variables:

L (float) – The total length of the path.

V(x)

The potential as a function of the distance x along the path.

dV(x)

dV/dx as a function of the distance x along the path.

d2V(x)

d^2V/dx^2 as a function of the distance x along the path.

pts(x)

Returns the path points as a function of the distance x along the path. Return value is an array with shape (len(x), N_dim).

fullTunneling

fullTunneling(path_pts, V, dV, maxiter=20, fixEndCutoff=.03, save_all_steps=False, verbose=False, V_spline_samples=100, tunneling_class=tunneling1D.SingleFieldInstanton, tunneling_init_params={}, tunneling_findProfile_params={}, deformation_class=Deformation_Spline, deformation_init_params={}, deformation_deform_params={})

Calculate the instanton solution in multiple field dimension.

This function works by looping four steps:

1. Fit a spline to the path given by phi.
2. Calculate the one-dimensional tunneling along this path.
3. Deform the path to satisfy the transverse equations of motion.
4. Check for convergence, and then go back to step 1.

Parameters:

• path_pts (array_like) – An array of points that constitute the initial guess for the tunneling path, with shape (num_points, N_dim). The first point should be at (or near) the lower minimum (the minimum to which the field is tunneling), and the last point should be at the metastable minimum.
• dV (V,) – The potential function and its gradient. Both should accept input of shape (num_points, N_dim) and shape (N_dim,).
• maxiter (int, optional) – Maximum number of allowed deformation / tunneling iterations.
• save_all_steps (bool, optional) – If True, additionally output every single deformation sub-step.
• verbose (bool, optional) – If True, print a message at the start of each step.
• callback (callable) – User supplied function that is evaluted just prior to deforming the path. Should return True if the path should be deformed, and False if the deformation should be aborted. Should accept 4 arguments: a SplinePath instance which describes the tunneling path, a tunneling object (instance of tunneling_class), the profile found by the tunneling object, and extra callback data.
• callback_data (any type) – Extra data to pass to the callback function if there is one. If this function is called from transitionFinder.findAllTransitions(), the callback data is the tunneling temperature.

Other Parameters:  

• V_spline_samples (int, optional) – Passed to SplinePath. If None, no second derivative will be passed to the tunneling class, and it will instead be evaluted using finite differences.
• tunneling_class (class, optional) – Either tunneling1D.SingleFieldInstanton or a subclass.
• tunneling_init_params (dict, optional) – Extra parameters to pass to the tunneling class.
• tunneling_findProfile_params (dict, optional) – Extra parameters to pass to tunneling_class.findProfile().
• deformation_class (class, optional) – Either Deformation_Spline or Deformation_Points, or some other object that exposes the same interface.
• deformation_init_params (dict, optional) – Extra parameters to pass to the deformation class.
• deformation_deform_params (dict, optional) – Extra parameters to pass to deformation_class.deformPath().

Returns:

• profile1D (namedtuple) – The return value from tunneling_class.findProfile().
• Phi (array_like or list) – The points that constitute the final deformed path. They are in one-to-one correspondence with the points in profile1D.
• action (float) – The Euclidean action of the instanton.
• fRatio (float) – A ratio of the largest transverse force on the final path relative to the largest potential gradient. This would be zero if the solution were perfect.
• saved_steps (list) – A list of lists, with each sub-list containing the saved steps for each deformation. Only written to if save_all_steps is True.

Examples

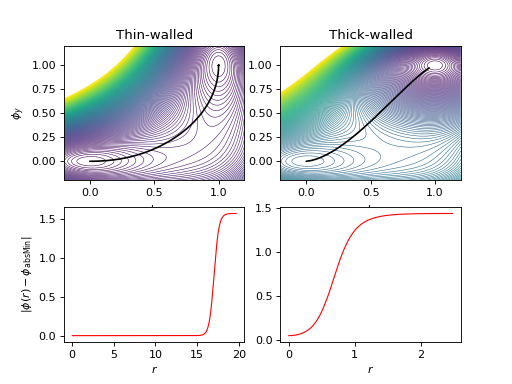
The following code shows typical usage for fullTunneling(). Most of the code is in setting up the potentials and plotting; it only takes one line to actually calculate each instanton.

import numpy as np
import matplotlib.pyplot as plt

from cosmoTransitions import pathDeformation as pd


class Potential:
    """
    A sample potential. The depth of the absolute minimum is controlled with
    the parameters `fx` and `fy`.

    This potential has no physical significance whatsoever.
    """
    def __init__(self, c=5., fx=10., fy=10.):
        self.params = c,fx,fy

    def V(self, X):
        """
        This is a two-dimensional potential, so the input should be some
        array with a *last* axis of length 2. That is, the final index in the
        array should always be the one that specifies the field (in this case
        *x* or *y*). This is the convention that CosmoTransitions uses
        throughout.
        """
        x,y = X[...,0], X[...,1]
        c, fx, fy = self.params
        r1 = x*x+c*y*y
        r2 = c*(x-1)**2 + (y-1)**2
        r3 = fx*(0.25*x**4 - x**3/3.)
        r3 += fy*(0.25*y**4 - y**3/3.)
        return r1*r2 + r3

    def dV(self, X):
        """
        The output of the gradient should have the same shape as the input.
        The last index specifies the direction of the gradient.
        """
        x,y = X[...,0], X[...,1]
        c, fx, fy = self.params
        r1 = x*x+c*y*y
        r2 = c*(x-1)**2 + (y-1)**2
        dr1dx = 2*x
        dr1dy = 2*c*y
        dr2dx = 2*c*(x-1)
        dr2dy = 2*(y-1)
        dVdx = r1*dr2dx + dr1dx*r2 + fx*x*x*(x-1)
        dVdy = r1*dr2dy + dr1dy*r2 + fy*y*y*(y-1)
        rval = np.empty_like(X)
        rval[...,0] = dVdx
        rval[...,1] = dVdy
        return rval

    def plotContour(self):
        nx = 100
        X = np.linspace(-.2,1.2,nx)[:,None] * np.ones((1,nx))
        Y = np.linspace(-.2,1.2,nx)[None,:] * np.ones((nx,1))
        XY = np.rollaxis(np.array([X,Y]), 0, 3)
        Z = self.V(XY)
        plt.contour(X,Y,Z, np.linspace(np.min(Z), np.max(Z)*.3, 200),
                    linewidths=0.5)


def makePlots():
    # Thin-walled instanton
    plt.figure()
    ax = plt.subplot(221)
    m = Potential(c=5, fx=0., fy=2.)
    m.plotContour()
    Y = pd.fullTunneling([[1,1.],[0,0]], m.V, m.dV)
    ax.plot(Y.Phi[:,0], Y.Phi[:,1], 'k', lw=1.5)
    ax.set_xlabel(r"$\phi_x$")
    ax.set_ylabel(r"$\phi_y$")
    ax.set_title("Thin-walled")
    ax = plt.subplot(223)
    ax.plot(Y.profile1D.R, Y.profile1D.Phi, 'r')
    ax.set_xlabel("$r$")
    ax.set_ylabel(r"$|\phi(r) - \phi_{\rm absMin}|$")

    # Thick-walled instanton
    ax = plt.subplot(222)
    m = Potential(c=5, fx=0., fy=80.)
    m.plotContour()
    Y = pd.fullTunneling([[1,1.],[0,0]], m.V, m.dV)
    ax.plot(Y.Phi[:,0], Y.Phi[:,1], 'k', lw=1.5)
    ax.set_xlabel(r"$\phi_x$")
    ax.set_title("Thick-walled")
    ax = plt.subplot(224)
    ax.plot(Y.profile1D.R, Y.profile1D.Phi, 'r')
    ax.set_xlabel("$r$")

    plt.show()

(Source code)

if __name__ == "__main__":
    makePlots()

(png, hires.png, pdf)

The callback function can be useful when this function is run from transitionFinder.findAllTransitions(). In that case, one doesn’t need to accurately calculate the tunneling path when one knows that the action is already below some threshold. For example, the following callback function will abort the deformation when action / T <= 120:

def callback(path, tobj, profile, T):
    action = tobj.findAction(profile)
    return action / T > 120